皆さんこんにちは、アンジェラケン(@anjeraken)です。

過去問はってどう言うふうに使うの?
今回はこういった疑問に答えていきます。
実際に解いた過去問の量
2021年に熊本大学自然科学教育学部、九州大学大学院システム情報科学府、大阪大学大学院工学研究科の3つの大学院の合格に向けて、過去問を解きまくりました。
熊本大学大学院の過去問をH18-R2年までの15年分。
九州大学大学院の過去問をH22-R2までの10年分。(H21年以前は傾向が変わっているため)
大阪大学大学院の過去問をH27-R3年の7年分解きました。
アンジェラケンの過去問の使い方
使い方は主に以下の7つの手順です。

- 過去問に目を通す
- 過去問の出題範囲の問題集を解く
- 過去問を解く
- わからないところの問題を解く
- ガチで過去問を解く
- 自信がないところを解く
- 過去問を何周もする
①過去問に目を通す
過去問に目を通して傾向を把握するのが、中で最初にして一番大切だと思います。
願書に書かれた出題範囲を見て勉強するよりも、どういった問題が出ているか傾向を見て問題を解くほうが、効率がいいです。
具体的にいうと、
とか
というのがわかります。
僕が経験したパターンとして大きく4つあると思います。
まずパターンは数学と専門で分かれます。
数学
- 毎年傾向が同じパターン
- まばらなパターン
専門
- 全体的に傾向が同じパターン
- 数年ごとに難易度問題傾向がガラッと変わるパターン
大体この4つだと思います。
実際にどんな感じかを見ていきましょう。
阪大はそこまで、傾向が変わっていないので、わかりやすい九大を例にしていきます。
【数学】傾向が同じだと判断するパターン
例として、九大のベクトルの問題4年分を比べてみましょう。(著作権の問題で、画像は貼り付けれないので、ちゃんとした問題が見たい方は、※のURLから問題を拝見してください。)
ベクトル
| 年 | R2のベクトル | R1のベクトル | H31のベクトル | H30のベクトル |
| 問題 | (1) (a)点Pが面に含まれることを示せ (b)Pにおける方線のなす角は? (2)面積分 | (1)3点で作られる平面と点Pとの距離は? (2)線積分 | (1)点Pにおけるスカラーφの勾配のベクトル場A方向成分は? (2)面積分 | 線積分と面積分 |
| 過去問 | ※ | ※ | ※ | ※ |
問題を見ると面積分または線積分が毎年出ています。
これから、間違いなく面積分・線積分を勉強して損はない。出る確率はかなり高いとわかります。
(1)は3次元空間の範囲で幅広く出題されており、出題されていない年もあるため、優先度的に面積分・線積分が優先されるべきです。
また(1)と(2)の問題はそれぞれ独立しており、関連性がないため、面積分・線積分だけわかれば点は取れます。
これよりベクトルの勉強は、面積分・線積分→他の範囲をざっとやっていく
といった流れを掴むことができます。
実際僕が受験した年のベクトルは面積分がピンポイントで3問でました。
とはいっても、ある程度テンプレートの証明問題があったり、ゴリむずの計算問題があったりするので、そういった細かいことは偉大な先輩たちの回答をみて傾向を把握していきましょう。
まずベクトルの答えを見てみましょう。
今回は限定的に面積分・線積分についてみていきます。




どうでしょうか?
なんとなく、回答を見ると問題の解き方が同じだと言うことがわかると思います。

最初にベクトルとかスカラー、式が与えられて、外積とか内積とかで積分するんだなぁ。
といった感じでわかると思います。
【数学】傾向がまばらなパターン
次に傾向がまばらで難易度に差があるパターンです。
例として、九大の線形代数を取り上げます。
線形代数
| 年 | R2の線形代数 | R1の線形代数 | H 31の線形代数 | H30の線形代数 |
| 問題 | (1)部分集合は? (2)条件が成り立つものを求めよ (3)ある条件の時、成り立つ証明 | (1)a_1-a_3まで計算 (2)行列Tを求めよ (3)Tの固有値固有ベクトル (4)線型結合系で表す (5)a_nを求めよ | (1)xを求めよ (2)yを求めよ (3)正則行列Pと対角行列Dは? (4)Pの逆行列は? (5)A^(10)を求めよ | (1)式が存在し、満たすことを示せ (2)式が成り立つことを証明せよ (3)条件が成り立つ時、成り立つ証明 |
| 過去問 | ※ | ※ | ※ | ※ |
問題を見るとなんとなく、R1とH31が計算系、R2とH30が「示せ。」と問題文にある証明系といった感じがわかると思います。
ベクトルほどのはっきりとした傾向がなく、行列の計算系に比べて証明系は難易度が高くなっています。
証明系の方が難易度が高い理由として、やり方さえ理解すればいい訳ではなく、深く定義や定理を知っておく必要があり、その時のヒラメキも大切になってきます。
また、(1)から最後まで、関連した問題になっており、(1)(2)あたりが解けないとキツいです。
これより、線形は基礎を固めて、定理や定義の把握もする必要がある。時間がかかる。といったことが分かります。



流し見しただけでも、全く回答のパターンが違うことが分かりますよね。
これより、線形代数は全体的に勉強する必要があるというのが、よりいっそ把握できたと思います。
【専門】傾向が同じパターン
例えば電気回路
全体的な傾向として、数学はあまり変わりませんが、専門はゴッソリ変わる時があります。
| 年 | R3 | R2 | H31 |
| 問題 | 問1:交流回路 問2:インピーダンス整合 問3:等価回路 問4:過渡現象 | 問1:交流回路 問2:インピーダンス整合 問3:等価回路 問4:過渡現象 | 問1:交流回路 問2:インピーダンス整合 問3:等価回路 問4:過渡現象 |
| 過去問 | ※ | ※ | ※ |
【専門】数年ごとにゴッソリと傾向が変わるパターン
専門教科の中で、数年ごとにゴッソリ傾向が変わることがあります。
おそらく専門科目は教授方が作っており、作る人が変わるからだと考えられます。
そのため、数年ごとに簡単になったりちょっと難しくなったり、激ムズになったりしています。
例えば九大の電磁気。
電磁気
| 年 | R3 | R2 | H31 | H30 |
| 問題 | 問1:直線同線(電界) 問2:球のコンデンサ(電界) 問3:有限直線同線(磁界) | 問1:点電荷(電界) 問2:点電荷(電界) 問3:円筒状電極(磁界) | 問1:平行平板コンデンサ(電界) 問2:同軸円筒ケーブル(磁界) 問3:ソレノイド(電磁波) | 問1:球のコンデンサ(電界) 問2:磁気回路(磁界) 問3:平行円平板コンデンサ(電磁波) |
| 過去問 | ※ | ※ | ※ | ※ |
電界、磁界、電磁波だったのに対し、H 31を境に電界2個と磁界1個になり簡単になっています。

よし!簡単になったけいけるぞ!

しかもまだ2年前やから今年もほぼかくで簡単やな!
そう思って試験に挑みました。
蓋を開けてみてびっくり。
めちゃくちゃ難しくなってました・・・
むず過ぎて半分解くのがやっとでした。。
問題が選択で、過去問がエグムズイなら

うん。これを選択するのは諦めよう。
と潔いのも大切です。
でないと僕みたいに爆死します。
僕の友達もかなり勉強した後に、選択するのを諦めて嘆いてました。

情報理論さ、過去問ゴリむずいんやけど。。

むずくなっとる、無理だわ。。

めっちゃ勉強したけど、他の科目選ぶわ。。
長い目でみたら間違いなくプラスなので勉強するに越したことはありません。
立ち直れる時間がある人はいいですが、時間がない人は気をつけてください。
こういったことにならないためにも傾向と対策はしっかりしておきましょう。
②過去問の出題範囲の問題集を解く
過去問の出題傾向の問題が把握できたら、次に出題範囲の問題集を解いていきます。
過去に出題されていた傾向の問題の範囲を解いていきます。
この繰り返しが効率がいいです。
まずベクトルについて、僕が使っていたマセマシリーズのベクトル解析で説明していきます。
マセマシリーズの特徴として、丁寧に詳しく分かりやすく定義や定理を説明してくれるため、ストーリー記憶として、定着し、理解も深まります。図も豊富で、字も読みやすくとても使いやすい参考書だと個人的に思います。
まず、講義4の線積分と面積分について勉強していきました。
途中にある例題を解答を見なくても解けるようになるまで、理解を深めました。
次にがっつり基礎からやるパターンの例として、線形代数について説明します。
とりあえず、マセマの線形代数を1周しました。
1周したといっても、ベッセル関数や核や虚像といった範囲は範囲外だったので、流す程度でやりました。
どこはやって、どこは関係ないからあまりやらないくて良いという判断をするときに、過去問が重要になってきます。
つまり、僕は1周するまでに、それぞれの単元ごとに過去問と照らし合わせながら、重要なとこと、そうでないとこを判断しています。
過去問見る→問題集→過去問をみる→…
です。
こんな感じで、専門分野や単元によっては、出題範囲が広かったり、基礎を理解する必要があったりして、全体を解くハメになることもあります。その時は基礎から解きましょう。
③過去問を解く(1周目)
問題集が終わったら実際にとけるか解いてみましょう。
最初は単元ごとにやっていくのがおすすめです。
例えば、線形代数の問題集を一通りやった後に、実際に線形代数の単元だけ解いてみる。
ベクトルの単元が終了したら、実際にベクトルの問題だけ解いてみる。
といった感じです。
ぼんやりと把握していた傾向をここで一気にしっかりとした傾向として把握できます。
ここで解く年数は10年前後とくのがいいと思います。
10年間見れば
特に専門。
できれば10年分ぐらい解きましょう。
勉強した単元のみを10年分ぐらい一気に解いていきます。
④分からないところを問題集・ネット・先輩の解答を見て調べて解く
過去問でできなかったところは、解き方が理解できるまで復習しましょう。
数学や専門分野や定理や原理が多く丸暗記だとかなりきついと思います。
それに、意味を理解していないと解けない問題が多々あります。
例えば、ベクトルのガウス積分。
ガウス積分の結果はそれぞれの面の外向きの発散の合計に一致します。
初めはガウス積分の意味を理解しておらず、そう言うものだと思っていました。
詳しい問題は忘れましたが、ある問題を解いている時、球の底面の部分があるかないかで答えが変わらないことをに気がつきました。
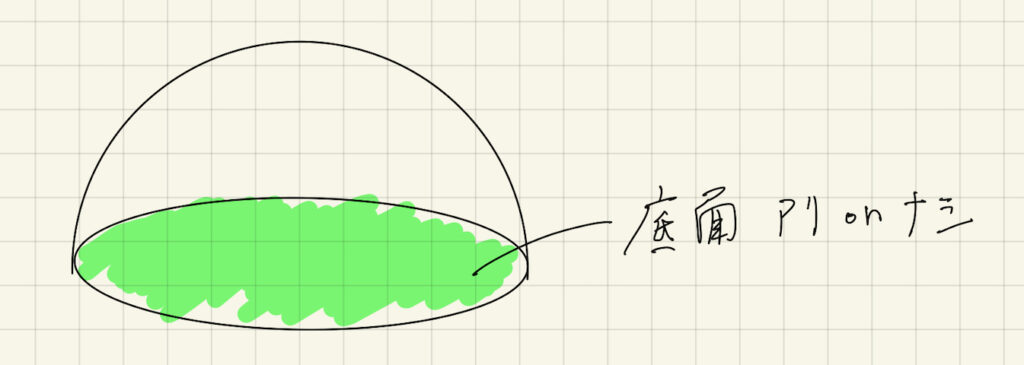

え?なんで?計算ミス?
色々と考え、マセマのベクトル解析をじっくり読み解いていきました。
結果、底面の面積分=0になることに気がつきました。
これにより、底面がない面積分と底面ありのガウス積分が一致するのだと理解しました。
数学は間違いなくYoutubeのヨビノリさんの動画が一押しです。
とにかくわかりやすい。
阪大の数学の微積の範囲が広くまた回転体の公式が多て困ってました。
例えばこの動画。
これを見れば、なぜその公式になったのか理解でき、ストーリー記憶として定着します。
そのため、公式自体を忘れたとしても、ストーリさえ思い出せば公式が作れちゃいます。
他にもラグランジュの未定数乗数法。
こういった積み重ねで、少しずつ理解を広げていくことが大切だと思います。
このために、過去問が優秀であるとかなり有利です。
それが一番効率がいいですからね。
⑤ガチで過去問を解く(2周目)
時間を測ってどれぐらいでとけるか、実際にやってみましょう。
できれば、1日で数学から専門までを1日で解くのが理想です。
そして残りの1日をやり直し、復習の時間に当てる。
これは本当に理想で実際は1日で終わらないです。
意外に解くのに時間がかかったり、忘れていたりするところが見つかります。

いや、1回解いたことある問題そんな忘れないでしょ。
これが、案外忘れてるものなんですよ。
解き方忘れに加えて、案外凡ミスも多いです。
実際に僕が2回目を解いた時の点数は以下のようなものでした。
| 年 | H 27 | H 28 | H 29 | H30 | H 31 | R2 | R3 |
| 数学 | 10.5/15 | 8/18 | 11.5/16 | 8/13 | 9.5/16 | 13/15 | / |
| 専門 | 8/13 | 12/15 | 15/20 | 14/18 | 15/20 | 10/19 | 20/21 |
全然満点じゃないんですよね^^;
実際は忘れていることよりも凡ミスの数の方が多いです。

マイナス忘れとったー!
とか

途中2乗つけ忘れて計算結果変わっとった。
とか

シンプルな計算ミスやん。
とか。
本番に向けて凡ミスをしない、見直しをする癖など些細なことですが、大事なことなので本番同様の緊張感を持って挑むと本番楽になります。
またやり直しも怠らずに。
どこで間違えたかを認識し同じ間違えをしないようにしましょう。
⑥自信がないところを重点的に
時間に余裕があれば、不安なところを潰していきましょう。
ここ自信ないな〜ってところを見つけたらって徹底的に潰しに行きます。
僕の場合は阪大の微積の範囲が毎年傾向が変わって不安でした。
特に、立体が被った部分の体積を積分で求める問題だったり、パラメータの回転体の体積・面積の求め方等です。
なので、参考書や問題集で、類似問題を解いて理解しているか確認しました。
またフーリエ変換の公式の証明方法やフーリエ級数の数学的帰納法を用いた証明方法に抜けてないかも不安になりました。
途中で、ちゃんと定義しているか、ぶっ飛んだ証明になってないかを確認しました。
⑦過去問を何周もする(3周目)
2周をしっかりこなせば、知識は十分だと思います。
あとは3周目で自信をつけていどみましょう。
3周目でも意外に忘れていることがあります。
なんせ7年分10年分ですからね^^;
ここまでやれば、合格できるはずです。
最後に
余談ですが、僕が受験した年から九大の選択する科目や科目のくくりが大きく変わりました。

出題された問題は例年通りで、内容自体はそこまで変わらなかったのですが、今回難易度の差がある例として取り上げた線形代数が選択から必須に変わりました。
そのため、難易度は下がって固有値固有ベクトル、対角化あたりの問題だろうと山を貼ってました。

今年から必須やけど、証明系も出るんな?。

いや〜でんでしょ。

でたら、みんな解けないよ。

やっぱそうよね〜。

流石に出してこんか。

だよ。でたら大量爆死よ。

試験当日。
数学の問題が配られて、線形代数は大門1なので、表紙の裏に印刷されているのが分かりました。
表紙から透けて証明問題が見えました。。

オワタ\(^o^)/
ゴリゴリ証明で爆死しました。
つまり選択科目が変わっても、いい意味でも悪い意味でも傾向が変わらないので、過去問の傾向チェックは怠らずにやりましょう。
また過去問は手に入れた年数よりも、過去問の使用量の方が大切です。
しっかり使い回しましょう。
今回は院試の合格率を上げるために私が実践した過去問の使い方7つの手順について紹介しました。
アンジェラケンはあなたを応援しています。
頑張ってください。( `・∀・)ノ



コメント